
1. 이상값 처리

▶ matplotlib 라이브러리
: 라이브러리 안에 다양한 모듈이 있음
: 그중 pyplot 모듈은 MATLAB(공학용 도구로 유명함)과 비슷한 명령어 스타일로 동작하는 함수 모음
: pyplot 모듈의 함수를 사용해 간편하게 그래프를 그리고 수정
: 기본 그래프 그리기 → plot()함수

▶ 라이브러리 설치 및 가져오기
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
▶ 데이터셋 불러오기
titanic = pd.read_csv('./datasets/titanic.csv')
titanic
2. 이상값 시각화하기
▶ 박스플롯 시각화
: 데이터를 동일한 사이즈의 4개 그룹으로 나누는 사분위수를 사용해 데이터의 모양 보여줌
: 박스의 제 1사분위수와 3사분위수는 25번째와 75번째 백분위수
: 박스 중간 선은 제 2사분위수로 중앙값(median)
: 박스 양 끝은 각각 최소(Minimum)와 최대(Maximum) → 이 범위를 벗어난 값은 이상값
: 이상값을 확인하는 가장 쉬운 방법은 데이터를 시각화하여 변수의 분포를 살펴보는 것
: 1개 변수에 관한 이상값 시각화 도구는 일반적으로 박스플롯이나 히스토그램 사용
: 2개 변수 간의 이상값을 찾을 때는 산점도 활용
▶ 박스플롯으로 이상값 확인
* 타이타닉 데이터셋의 Fare 변수를 대상으로 확인
sns.set_theme(style = "whitegrid")
plt.figure(figsize = (12, 4)) # 12x4인치
sns.boxplot(x = titanic.Fare, color = 'red');
>> ㅣㅡㅣ의 바깥 부분인 70쯤 이후부터가 이상값
* 타이타닉 데이터셋의 Age 변수를 대상으로 확인
plt.figure(figsize = (12, 4))
sns.boxplot(x = titanic.Age, color = 'skyblue')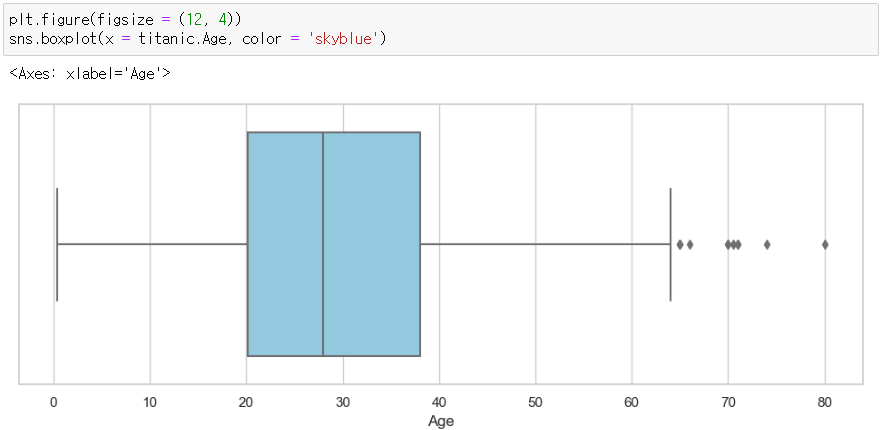
>> ㅣㅡㅣ의 바깥 부분인 60 초반쯤 이후부터가 이상값
3. IQR 기법으로 이상값 확인
▶ IQR 기법
: 시각화 기법으로 데이터의 이상값 분포를 본 뒤 실제 이상값을 추출할 때 사용
: 가장 고전적이고, 기초적이지만 많이 활용하는 기법
: 탐색적 데이터분석의 선구자인 존튜키가 개발한 전통적인 방법
▶ IQR 기법을 적용하는 순서
: 1사분위수 Q1 찾기
: 3사분위수 Q3 찾기
: IQR 계산 IQR = Q3 - Q1
▶ 함수로 이상값 확인
: 판다스의 결측값 찾기 함수처럼 이상값을 자동으로 추출해주는 함수는 없음
→ 사분위수 함수로 직접 이상값을 걸러내는 함수 정의해보기
def outlier_iqr(data, column):
# lower(ㅣㅡㅣ좌측 선 값, 하한), upper(ㅣㅡㅣ우측 선 값, 상한) 글로벌 변수 선언
global lower, upper
# 1, 3사분위수 지정
q1, q3 = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
# IQR 계산
iqr = q3 - q1
# 이상값 cutoff(기준점) 계산
cut_off = iqr * 1.5
# lower와 upper 구분값 구하기
lower, upper = q1 - cut_off, q3 + cut_off
print('IQR은', iqr, '이다.')
print('lower 기준값은', lower, '이다.')
print('upper 기준값은', upper, '이다.')
# lower와 upper를 넘어서는 데이터 각각 저장
data1 = data[data[column] > upper]
data2 = data[data[column] < lower]
# 이상값 총 개수 구하기
return print('총 이상값 개수는', data1.shape[0] + data2.shape[0], '이다.')outlier_iqr(titanic, 'Fare')
▶ 이상값의 범위 시각화
plt.figure(figsize = (12, 7))
sns.distplot(titanic.Fare, bins = 50, kde = False)
plt.axvspan(xmin = lower, xmax = titanic.Fare.min(), alpha = 0.2, color = 'pink')
plt.axvspan(xmin = upper, xmax = titanic.Fare.max(), alpha = 0.2, color = 'yellow')
plt.show();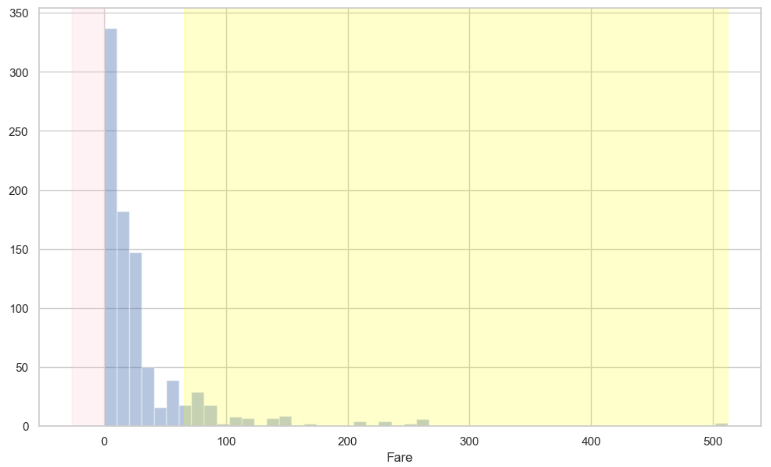
4. 이상값 처리
4-1) 이상값 삭제하기
▶ 정상 범주 데이터 = (위 함수의) lower 값보다 큰 데이터 + upper 값보다 작은 데이터
titanic_not_outlier = titanic[(titanic['Fare'] > lower) & (titanic['Fare'] < upper)]
titanic_not_outlier.head()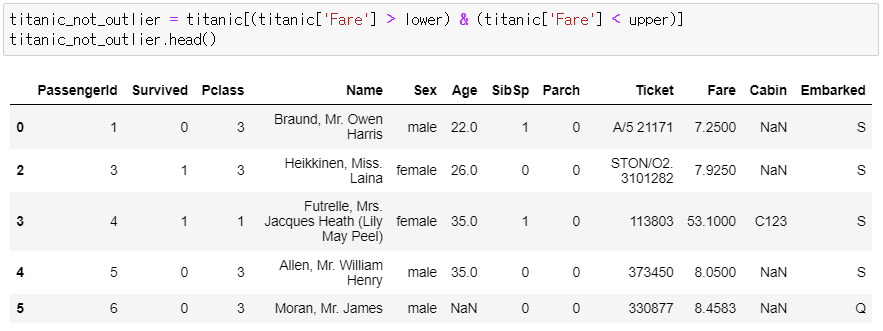
▶ 이상값이 제외된 데이터의 수
len(titanic_not_outlier)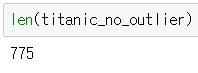
4-2) 이상값 대체
: 이상값을 삭제하는 대신 평균값으로 변경하는 방법
: 이상값의 인덱스를 파악한 뒤 타이타닉 원본 데이터에서 이상값에 해당하는 인덱스만 지정하여 그 값을 해당 변수의 평균값에 저장
▶ upper 값을 벗어나는 데이터(이상값) 출력
: 틸데(~) 기호를 활용해서 선택
outlier = titanic[(titanic['Fare'] > lower) & ~(titanic['Fare'] < upper)]
outlier.head()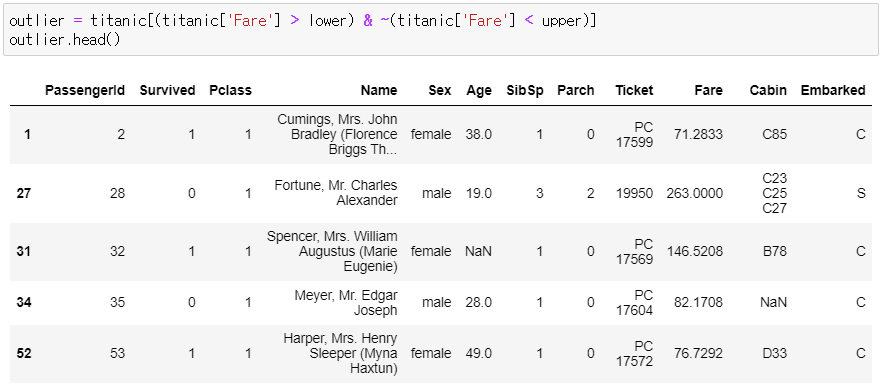
▶ 이상값 인덱스 출력
outlier_index = [outlier.index]
outlier_index
▶ 이상값의 인덱스 값을 평균값으로 다시 저장
: (0부터 시작) 9번째 열인 Fare의 값을 평균값으로 저장
: 'Fare'의 평균값은 32.204208임
titanic.iloc[outlier_index, 9] = titanic['Fare'].mean()
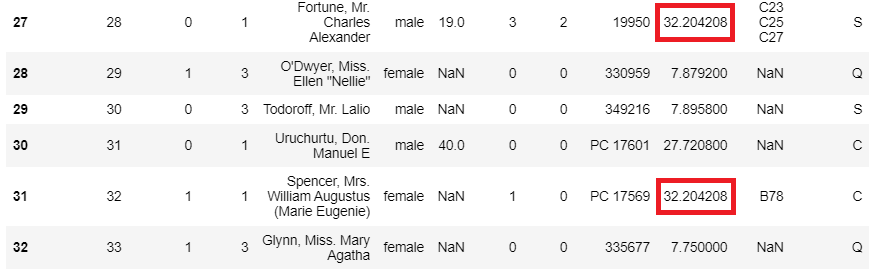
▶ 이상값 변경 확인
titanic.head(50)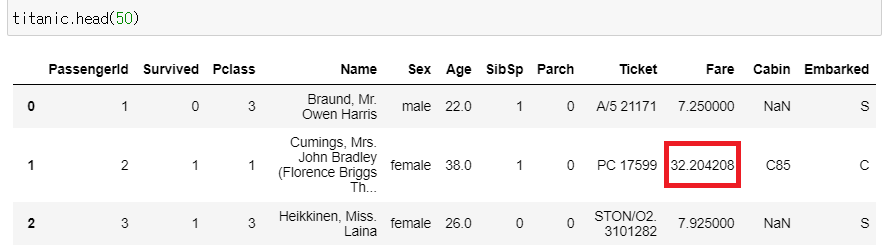
...
...
>> 뒤에 데이터 더 있음(50개의 데이터를 뽑았으니 인덱스 49번까지 출력됨)
▶ 변경한 데이터 저장
titanic.to_csv('./datasets/titanic2.csv')




댓글