머신러닝 | 로지스틱 회귀(Logistic Regression) 모델 | 모델 평가지표 (Accuracy, F1-score) | 지도학습 | 분류분석(Y변수가 범주형 데이터일 때 사용

 

1. 선형회귀와 로지스틱 회귀 비교

 

▶ 선형회귀와 로지스틱 회귀의 공통점

• 모델 생성이 쉬움
• 가중치(혹은 회귀계수)를 통한 해석이 쉬운 장점이 있음
• X변수에 범주형, 수치형 변수 둘 다 사용 가능

 

▶ 선형회귀와 로지스틱 회귀의 차이점

	선형회귀(회귀)	로지스틱 회귀(분류)
Y(종속변수)	수치형	범주형
평가척도	Mean Squared Error R square(선형회귀의 경우만)	Accuracy F1-score
sklearn 모델 클래스	sklearn.linear_model.linearRegression	sklearn.linear_model.LogistricRegression
sklearn 평가 클래스	sklearn.metrics.mean_squared_error skelarn.metrics.r2_score	sklearn.metrics.accuracy_score skelearn.metrics.f1_score

---

2. 로지스틱 회귀 이론

 

▶ Y가 범주형 변수일 때 선형함수가 가지는 한계

: Y는 범주형 변수 → 예를 들어, Y가 0 아니면 1 (모 아니면 도)

: X가 연속형 변수이고, Y가 특정 값(위 예시에서는 0아니면 1)이 될 확률이라고 설정해보자.

: 만약 선형함수(y = w0 + w1X)를 적용하면 확률은 0과 1 사이인데 예측값이 확률 범위를 넘어갈 수 있는 문제가 있음

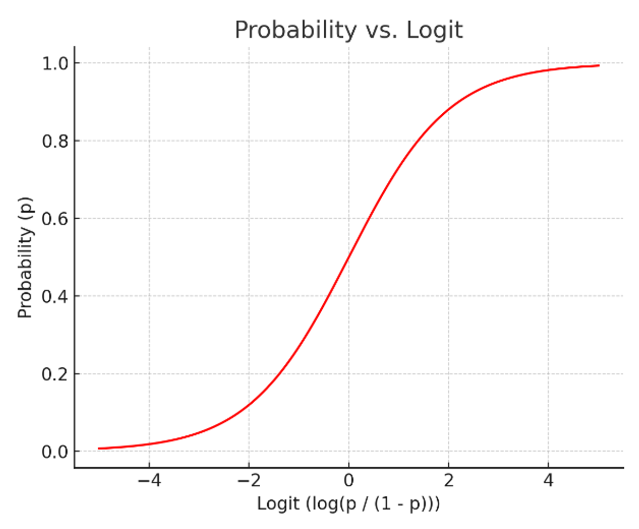
: 그런데 만약 S자 그래프 함수를 적용하면 Y변수 값을 그나마 잘 설명할 수 있게 됨

: 이 S자 그래프 함수가 로지스틱 회귀함수임

 

▶ 로짓 개념의 등장

: 위 S자 그래프 함수를 만들기 위한 개념

 

① 오즈비(Odds ratio)

: 승산비

: 실패확률 대비 성공확률

: 성공확률 / 실패확률  = P / 1 - P

: 도박사들이 자주 쓰는 개념

• 예를 들어, 도박이 성공할 확률이 80%면, 오즈비는 80% / 20% = 4
• 다시 말해, 도박이 1번 실패하면 4번은 딴다는 말

: P가 증가할수록 오즈비가 급격하게 증가하는 특성이 있음 → 선형성을 따르지 않게 됨

확률이 증가할수록 오즈비는 급격히 발산

 

② 로짓(Logit)

: 오즈비에 log(로그)를 씌워 완화해준 것

• P는 0과 1 사이의 값이기 때문

: 로짓의 그래프가 더 선형적인 그림을 나타내어 선형회귀의 기본식을 활용할 수 있게 됨

• 로지스틱 '회귀'라고 불리는 이유가 이것 때문

확률이 증가할수록 로짓은 완만히 증가

 

③ 로지스틱 함수

: 로짓 그래프의 X-Y축을 교체

: 어떤 값을 가져오더라도 반드시 특정 사건이 일어날 확률(Y값이 특정 값일 확률)이 0과 1 안으로 들어오게 함

: 가중치 값을 알면 X값이 주어졌을 때 해당 사건이 일어날 수 있는 확률 P를 계산할 수 있게 됨

• 이 때 확률 0.5를 기준으로
  높으면 사건이 일어남 P(Y) = 1
  낮으면 사건이 일어나지 않음 P(Y) = 0 으로 판단하여 분류 예측에 사용함

: 시그모이드 함수 중 하나로 딥러닝에서도 활용됨

 

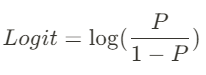
(참고) P에 대하여 정리

---

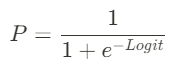
: 로짓과 기존 선형회귀의 우변을 합쳐 다음과 같은 식을 도출

 

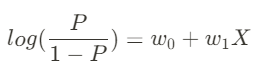
: 양 변에 자연지수 e를 취해 다음과 같은 식을 도출

 

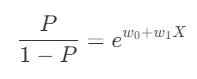
(해석) X값이 w1만큼 증가하면 오즈비는 e^w1 (e의 w1제곱)만큼 증가한다.

---

3. 분류 평가 지표(정확도, F1-Score)

 

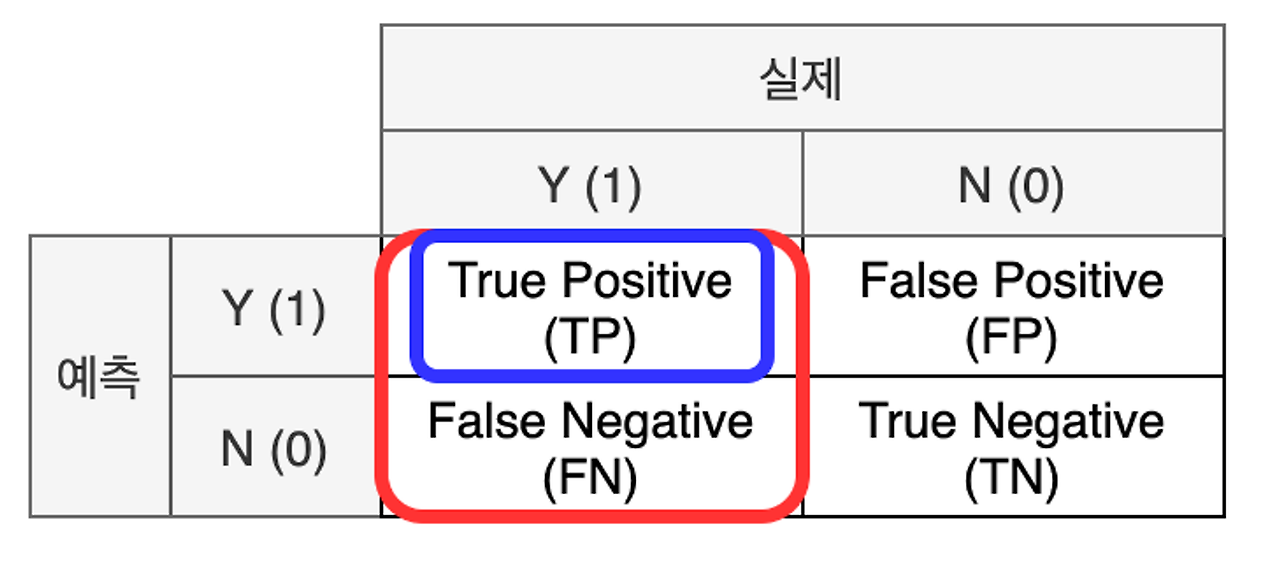
▶ 혼동행렬 (Confusion Matrix)

: 실제 값과 예측 값에 대한 모든 경우의 수를 표현하기 위한 2x2 행렬

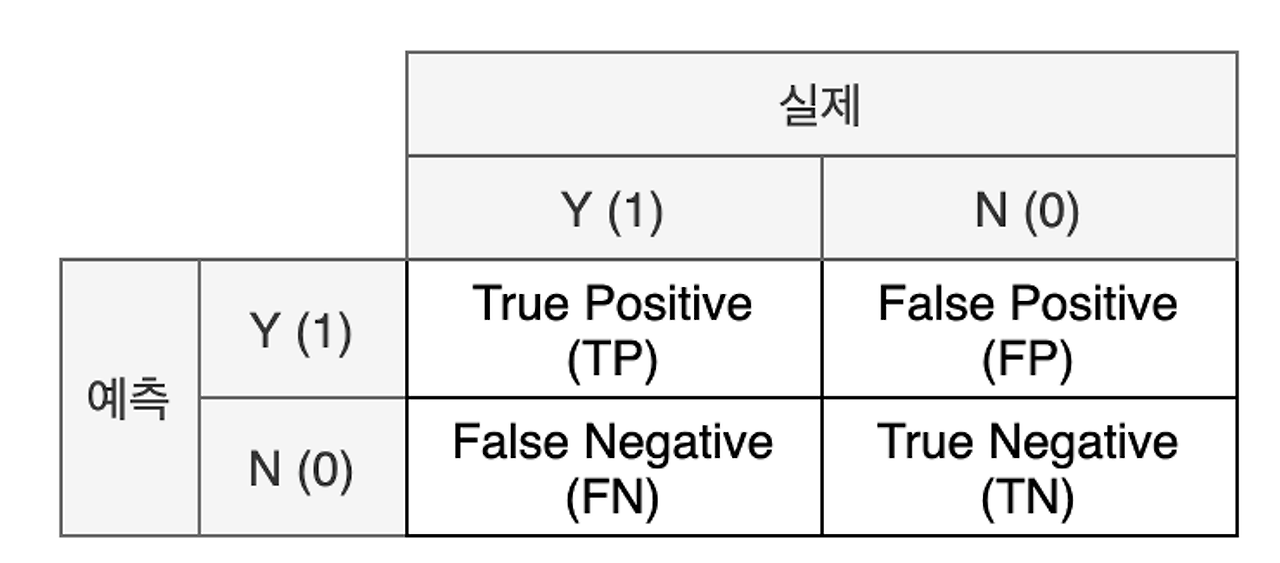
• 표기법
  • True : 실제와 예측이 같을 때
    False : 실제와 예측이 다를 때
  • Positive : 예측을 양성으로 판단했을 때
    Nagative : 예측을 음성으로 판단했을 때
• 해석
  • TP : 예측을 양성(Positive)이라고 했고, 실제와도 같음(True)
  • FP : 예측을 양성(Positive)이라고 했는데, 실제와는 다름(False) → 실제는 음성이었음(예측실패)
  • TN : 예측을 음성(Nagative)이라고 했고, 실제와도 같음(True)
  • FN : 예측을 음성(Nagative)이라고 했는데, 실제와는 다름(False) → 실제는 양성이었음(예측실패) 

---

▶ 모델 평가 지표

 

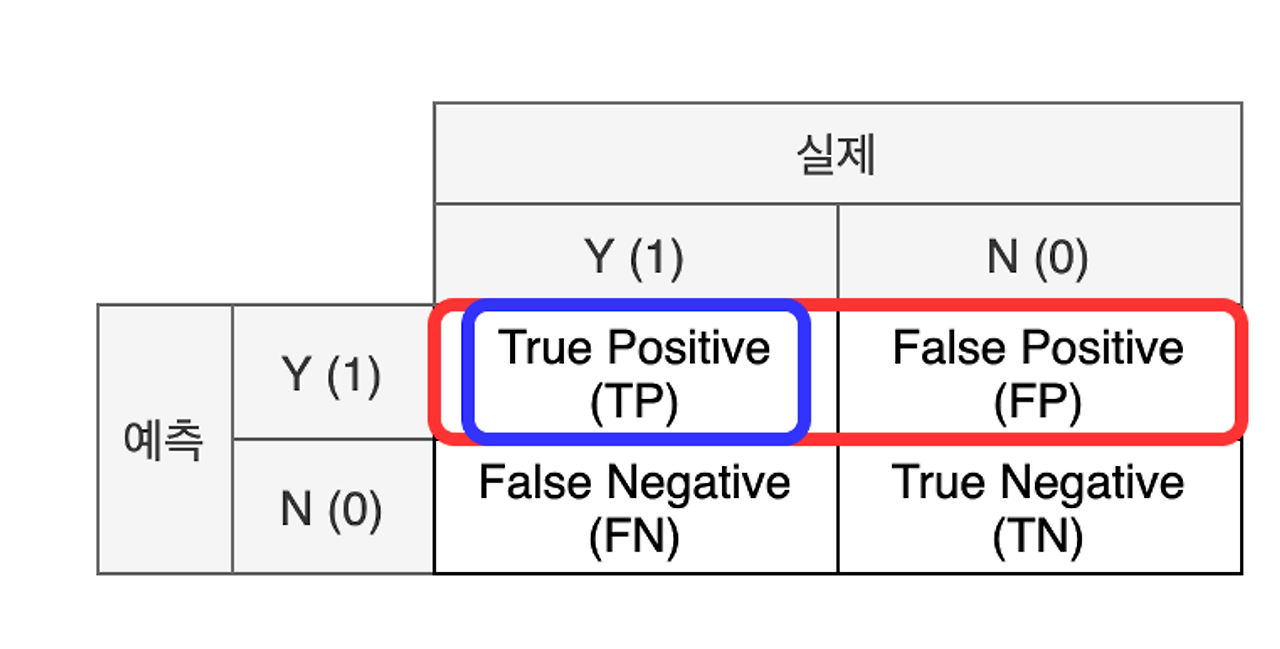
① 정밀도(Precision)

: (모델 관점) 모델이 양성으로 예측한 결과 중 실제 양성의 비율

정밀도(precision) = TP / (TP + FP)

 

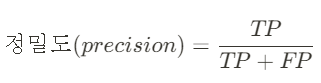
② 재현율(Recall)

: (데이터 관점) 실제 값이 양성인 데이터 중 모델이 양성으로 예측한 비율

재현율(recall) = TP / (TP + FN)

 

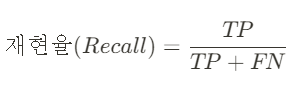
③ F1-Score

: 정밀도와 재현율의 조화평균

 

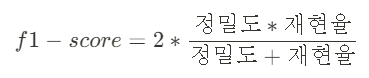
④ 정확도(Accuracy)

: 전체 경우의 수 중 실제와 예측값이 일치한 정도

 

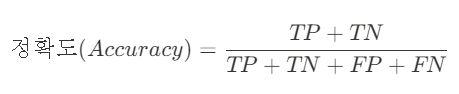
■ 정확도의 한계 / F1-Score를 같이 보는 이유

 

: 어떤 사람이 모든 환자를 정상이라고 판정하는 날림 '암 진단 모델'을 만들었음

• 암 진단 모델: 무조건 환자를 음성(정상인)이라고 판정함
  • 100명의 환자 중
    95명은 음성(정상)
    5명은 양성(암 환자)
  • 날림 '암 예측 모델'에 따르면 95%를 맞춘 꼴이 됨
  • 실제로는 양성(암 환자)을 하나도 가려내지 못함
    • TP : 실제 암 환자인데, 양성(암 환자)이라고 올바르게 분류한 경우 → 0명
    • FP : 실제 정상인데, 양성(암 환자)으로 잘못 분류한 경우 → 0명
    • TN : 실제 정상인데, 음성(정상)이라고 올바르게 분류한 경우 → 95명
    • FN : 실제 암 환자인데, 음성(정상)이라고 잘못 분류한 경우 → 5명
      • 정밀도는 정의되지 않음(division by zero), 재현율은 0
      • 정확도는 95% 
      • F1-Score는 0

: 상단 예시처럼 특히 Y값의 비율이 불균형한 경우에는

  정확도가 제 기능을 하지 못하게 되고,

  이를 보완하기 위해 Y범주의 비율을 맞춰주거나, F1-Score를 사용함

---

4. 로지스틱 회귀 정리

 

▶ 로지스틱 회귀

: 로지스틱 회귀는 선형회귀의 아이디어에서 종속 변수(Y)만 가공한 것이기 때문에 선형회귀의 장, 단점을 똑같이 가짐

• 장점
  
  • 직관적이며 이해하기 쉬움
• 단점
  • 복잡한 비선형 관계를 모델링하기 어려울 수 있음
• 사용하는 Python 패키지
  • sklearn.linear_model.LogisticRegresson