
1. 선형회귀 이론
▶ 선형회귀 용어 정리
- X는 독립변수, 원인변수, 설명변수
- Y는 종속변수, 결과변수
▶ 통계학에서 사용하는 선형회귀 식

β0 : 편향(Bias)
β1 : 회귀 계수
ε : 오차(에러), 모델이 설명하지 못하는 Y의 변동성
>> 수식 계산 방법 : 각 변수는 사실 행렬로 이루어진 값이라서 행렬 계산함

▶ 머신러닝 / 딥러닝에서 사용하는 선형회귀 식

ω : 가중치
b : 편향(Bias)
▶ 두 수식의 의미
- 일차방정식 Y = aX+b
- 산재되어 있는 데이터 값들을 가장 잘 나타내주는 하나의 '직선'을 그리는 것
- 회귀 계수(혹은 가중치)의 값을 알면 X가 주어졌을 때 Y를 알 수 있음
2. 최적의 직선을 그리는 법
2-1) X와 Y 간의 상관관계 찾아내기
- 조사하고 싶은 X와 Y 결정하기
- 키(X)가 크면 몸무게(Y)가 많이 나갈 것이다.
- 기온(X)이 높아지면 아이스크림 판매량(Y)이 많아질 것이다.
- X와 Y의 상관관계를 구해보기
- Scatter Plot 등으로 시각화해서 상관 정도 살펴보기
▶ (예시) 키(X)와 몸무게(Y)의 상관관계 확인하기
① 필요한 라이브러리 임포트
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
② 임의로 설정한 키와 몸무게 데이터
heights = [158,167,163,173,168,154,166,161,163,165]
weights = [47,51,52,62,60,41,56,46,49,49]
③ 데이터프레임 만들기
body_df = pd.DataFrame({'Heights' : heights,
'Weights' : weights})
body_df
④ 상관관계 정도 시각화해보기(Scatter Plot)
sns.scatterplot(data = body_df, x = 'Heights', y = 'Weights')
plt.title('Height vs. Weight')
plt.xlabel('Height(cm)')
plt.ylabel('Weight(kg)')
2-2) 데이터들을 가장 잘 설명하는 직선 찾기
- 직선 그려보기
- 직선과 각 데이터값 사이의 거리 계산하기
- 실제 데이터 값 - 직선의 예측 값 = Error
- ∑ (실제 데이터 값-직선의 예측값)
→ Error를 최소화 하는 직선을 찾으면 됨
- 그런데,
어떤 데이터는 직선(예측값)보다 위에 있어서 Error가 양수가 되고,
어떤 데이터는 직선(예측값)보다 아래에 있어서 Error가 음수가 되어
위의 거리 계산 값을 모두 더하면, 서로 상쇄되는 문제가 있음- 각 데이터의 Error 값들을 제곱한 뒤에 모두 더해주기
- ∑ (실제 데이터 값 - 직선의 예측값)^2
→ Error를 제곱해서 합한 값을 최소화 하는 직선을 찾으면 됨
- 그런데,
나중에는 데이터를 더 수집할 예정인데, 데이터가 늘어나면 Error값도 자연스럽게 커질 수밖에 없음- Error를 제곱하고 더한 값을 데이터의 개수로 나누기
∑ (Error)^2 / n
→ (Error 제곱합)을 데이터 개수로 나눈 값(MSE)을 최소화하는 직선을 찾으면 됨 - 데이터를 제곱하면서 뻥튀기 된 단위도 다시 제자리로 돌려놓기 위해 √ root 씌워주기
- √ (∑ (Error)^2 / n)
→ MSE에 루트를 씌운 것은 RMSE라고 불림
- Error를 제곱하고 더한 값을 데이터의 개수로 나누기
▶ (예시) 키와 몸무게 데이터를 가장 잘 나타내는 직선 찾기
① 직선 그려보기
# 선형회귀 라이브러리 임포트
from sklearn.linear_model import LinearRegression
# 선형회귀 모델 가져오기
model_lr = LinearRegression()# X, y값 설정해주기
X = body_df[['Heights']]
y = body_df[['Weights']]
# X와 y데이터를 모델에 넣어 훈련
model_lr.fit(X=X, y=y)
# 가중치(w1)
print(model_lr.coef_)
# 편향(bias, w0)
print(model_lr.intercept_)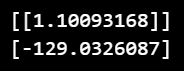
# w1은 회귀계수, w0는 편향
w1 = model_lr.coef_[0][0]
w0 = model_lr.intercept_[0]
print('y = {}x + {}'.format(w1.round(2), w0.round(2)))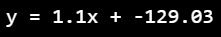
- 키와 몸무게 데이터에 대한 선형회귀 식
y = 1.1x + -129.03 - 이 식의 의미는 키가 1cm 커질 때마다 몸무게가 1.1kg씩 증가한다고 해석할 수 있음
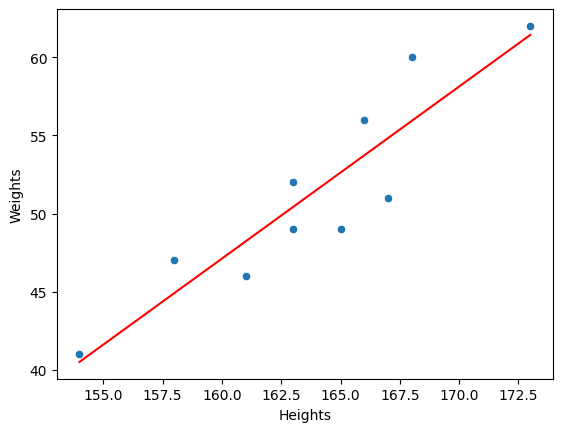
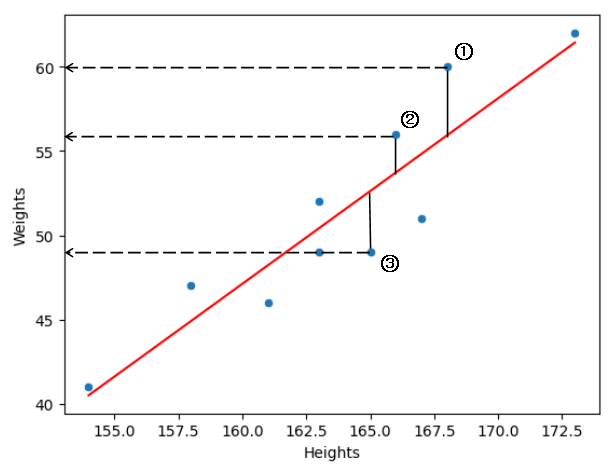
② 직선과 각 데이터 값 사이의 거리 계산해보기
- ①번 실제 데이터 = 60 / 예측 데이터 = 56 / Error = +4
- ②번 실제 데이터 = 56 / 예측 데이터 = 54 / Error = +2
- ③번 실제 데이터 = 49, 예측 데이터 = 53 / Error = -4
# 예측 데이터
body_df['pred'] = w1*body_df['Heights'] + w0
body_df# 에러
body_df['error'] = body_df['Weights'] - body_df['pred']
body_df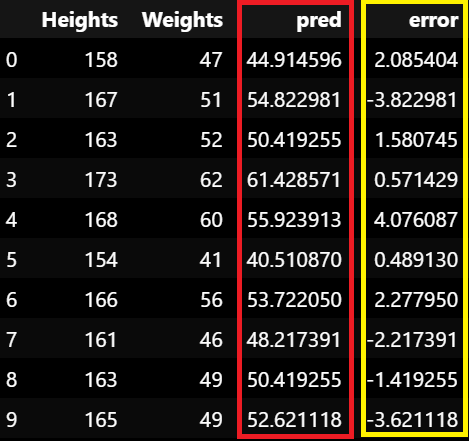
③ 각 Error를 제곱해서 모두 더하기
- ①,②,③의 제곱 합: {(4)^2 + (2)^2 + (-4)^2} = 16 + 4 + 16 = 36
# 제곱
body_df['error^2'] = body_df['error']**2
body_df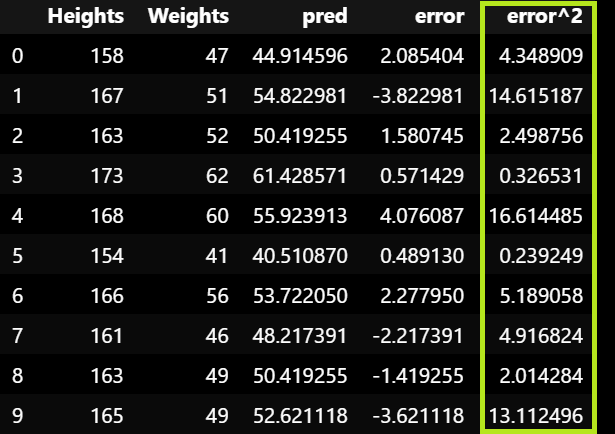
④ 전체 Error 합을 데이터 개수로 나누기
- ①,②,③ 데이터만 고려한다고 했을 때 36 / 3 = 12 → 이 값이 MSE
- √ root 씌워주기 √12 = 약 3.46
# 제곱합 나누기 데이터 개수 -> MSE
body_df['error^2'].sum() / len(body_df)
3. 회귀분석 평가 지표 (MSE, R Square)
3-1) MSE (Mean Squared Error)
- (참고)
y 값의 머리에 있는 ^ 표기는 hat이라고 부르는데, 예측(혹은 추정)한 수치를 나타낼 때 ^을 씌워줌
① Error = 실제 데이터 - 예측 데이터
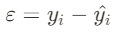
② 에러 제곱합 : ∑ (Error)^2
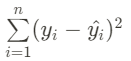
③ 에러 제곱합 / 데이터 개수 : ∑ (Error)^2 / n
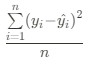
▶ 최종적으로 이 수식이 MSE (Mean Squared Error)임
머신러닝이든 딥러닝이든, 어떤 모델을 만들어도 이 MSE 지표를 최소화 하는 방향으로 진행하고, 평가될 것임
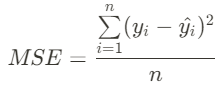
+ 기타 평가 지표
▶ RMSE
: MSE에 루트를 씌워 제곱 된 단위 다시 맞추기
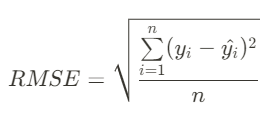
▶ MAE
: 제곱이 아니라 절대값을 이용해 오차 계산하기
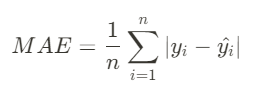
3-2) R Square
_선형회귀만의 평가지표
▶ R Square 지표
: 전체 모형에서 회귀선으로 설명할 수 있는 정도를 보여줌
: 어떤 값을 "예측" 한다는 것은 어림짐작으로 평균값보다는 예측을 잘 해야 한다는 것을 의미함
: 평균과 비교해서 회귀선이 실제 데이터값을 얼마나 더 잘 설명하고 있는지 확인
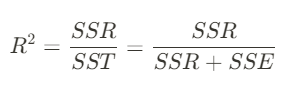
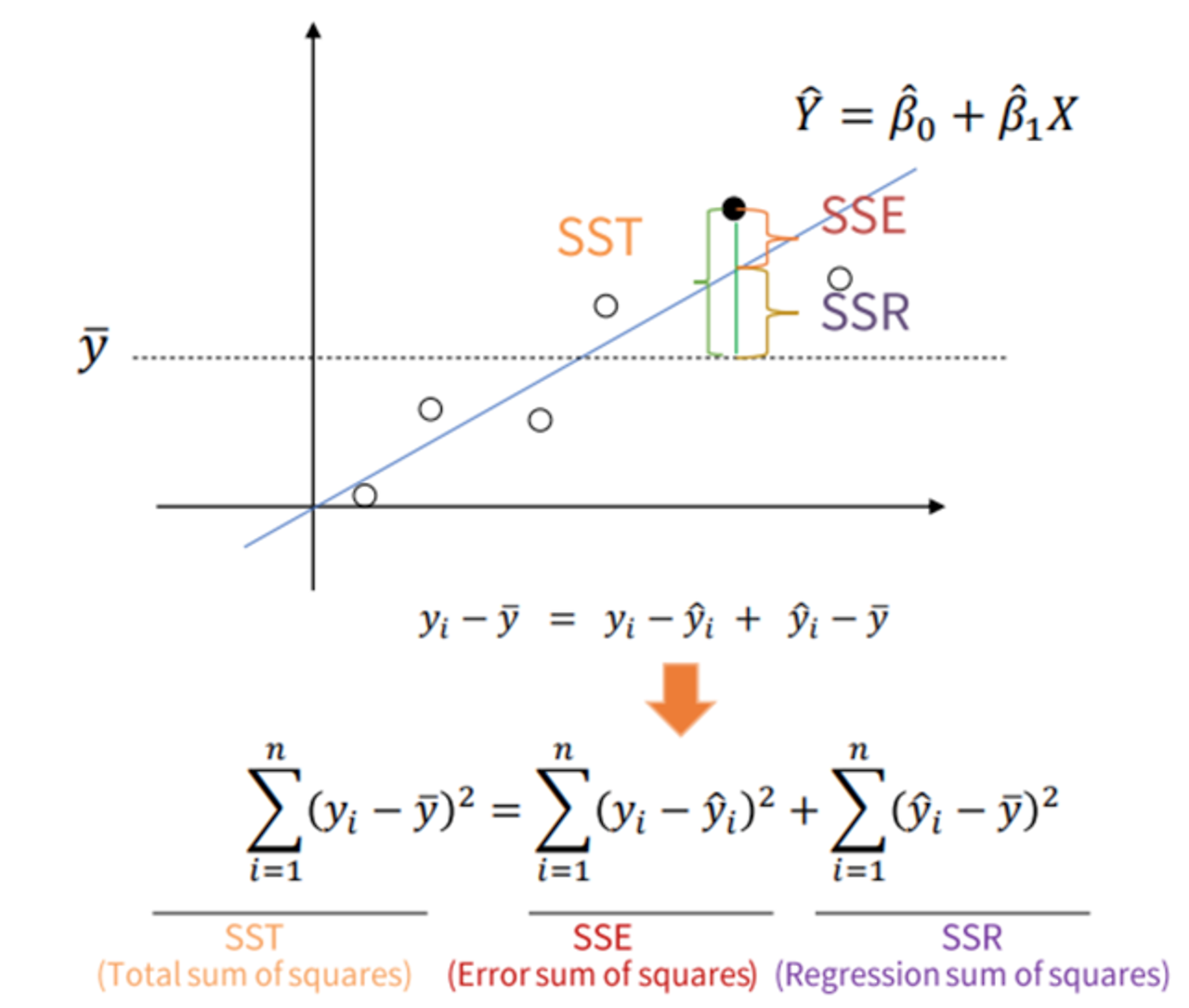
▶ SST, SSR, SSE의 개념
- SSR : 회귀선(예측값)이 평균에 비해 실제 데이터값을
- SSE : 회귀선(예측값)이 설명하지 못한 실제 데이터값과의 간극
- SST : SSR와 SSE를 합한 값, 평균이 설명하지 못한 실제 데이터값과의 간극
4. 선형회귀 적용
▶ 라이브러리 설치
- scikit-learn : Python 머신러닝 라이브러리
- numpy : Python 고성능 수치 계산을 위한 라이브러리
- pandas : 테이블 형 데이터를 다룰 수 있는 라이브러리
- matplotlib : 대표적인 시각화 라이브러리, 그래프가 단순하고 설정 작업 많음
- seaborn : matplotlib 기반의 고급 시각화 라이브러리, 상위 수준의 인터페이스를 제공
▶ 자주 쓰는 함수
- sklearn.linear_model.LinearRegression : 선형회귀 모델 클래스
- coef_ : 회귀 계수
- intercept_ : 편향(bias)
- fit : 데이터 학습
- predict : 데이터 예측




댓글