
5. 벡터의 내적과 외적
# 벡터의 내적과 벡터의 길이
▶ 벡터의 곱 혹은 그 결과를 만들기 위한 방법 두가지 : 내적, 외적
- 내적(Dot Product) : $\vec{a}·\vec{b}$ → 두 벡터를 곱해 스칼라 값을 가지게 됨
- 벡터의 길이(Length) : $||\vec{a}|| = \sqrt{a_{1}^2 + a_{2}^2 +...+ a_{n}^2}$ → 피타고라스 정리 생각하면 편함
# 벡터 내적의 성질 증명
각각의 성분에 대해서 일반적인 수에 대한 교환법칙, 분배법칙, 결합법칙이 벡터와 내적에서도 비슷하게 적용될 수 있음
▶ 교환법칙 : 내적에서는 곱의 순서가 중요하지 않음
- $\vec{v} · \vec{w} = \vec{w} · \vec{v}$
- $ \vec{v} · \vec{w} = v_{1}w_{1} + v_{2}w_{2} + ... + v_{n}w_{n} $
- $ \vec{w} · \vec{v} = w_{1}v_{1} + w_{2}v_{2} + ... + w_{n}v_{n} $
▶ 분배법칙
- $(\vec{v} + \vec{w}) · \vec{x} = (\vec{v} · \vec{x} + \vec{w} · \vec{x}) $
▶ 결합법칙
- $(c\vec{v} · \vec{w}) = c(\vec{v} · \vec{w})$
# 코시-슈바르츠 부등식의 증명
▶ 코시-슈바르츠 부등식
$\vec{x}, \vec{y} \in \mathbb{R}^n$ , 0이 아닌 벡터라고 가정
- $|\vec{x} · \vec{y}| ≤ ||\vec{x}|| \, ||\vec{y}||$ : 두 벡터의 내적이 두 벡터의 길이의 곱과 같거나 작음
- $|\vec{x} · \vec{y}| = ||\vec{x}|| \, ||\vec{y}||$ : 두 벡터의 내적이 두 벡터의 길이의 곱과 같아지는 경우는 하나의 벡터가 다른 벡터의 스칼라배인 경우 뿐임. (동일선상에 있는 경우)
# 벡터의 삼각부등식
ex) $\mathbb{R}^2$
- $||\vec{x} + \vec{y}||^2 ≤ ||\vec{x}||^2 + 2||\vec{x}||\,||\vec{y}|| + ||\vec{y}||^2$
- $||\vec{x} + \vec{y}||^2 ≤ (||\vec{x}|| + ||\vec{y}||)^2$
- $||\vec{x} + \vec{y}|| ≤ (||\vec{x}|| + ||\vec{y}||)$
→ 아무래도 돌아서 가는 거리보다 가로질러 가는 거리가 더 작을 것임

# 벡터 사이의 각 정의하기
▶ 삼각형의 조건 : 한 변의 길이는 나머지 길이의 합보다 작거나 같아야 함
$\vec{a}, \vec{b} \in \mathbb{R}^n, non\,zero$ : 영벡터이면서 $\mathbb{R}^2$의 원소인 실수 벡터
- $||\vec{a}|| ≤ ||\vec{a}-\vec{b}|| + ||\vec{b}||$
- $||\vec{b}|| ≤ ||\vec{a}-\vec{b}|| + ||\vec{a}||$
- $||\vec{a}-\vec{b}|| ≤ ||\vec{a}|| + ||\vec{b}||$
▶ 두 벡터의 내적의 관계 : 두 벡터의 내적은 벡터 길이의 곱과 같음

- $||\vec{a}-\vec{b}||^2 = ||\vec{b}||^2 + ||\vec{a}||^2 -2||\vec{a}||\,||\vec{b}||\, cos\theta$
- $(\vec{a}-\vec{b}) · (\vec{a}-\vec{b})$
$= \vec{a} · \vec{a} - \vec{a} · \vec{b} - \vec{b} · \vec{a} + \vec{b} · \vec{b}$
$= ||\vec{a}||^2 -2(\vec{a} · \vec{b}) + ||\vec{b}||^2$
$= ||\vec{b}||^2 + ||\vec{a}||^2 -2||\vec{a}||\,||\vec{b}||\, cos\theta$ - $(\vec{a} · \vec{b}) = ||\vec{a}||\,||\vec{b}||\, cos\theta$
- 두 벡터가 주어진다면, 이 공식을 통해 두 벡터 사이의 각도($cos\theta$)를 구할 수 있게 됨
▶ 두 벡터 사이의 각이 0º이거나 180º인 경우
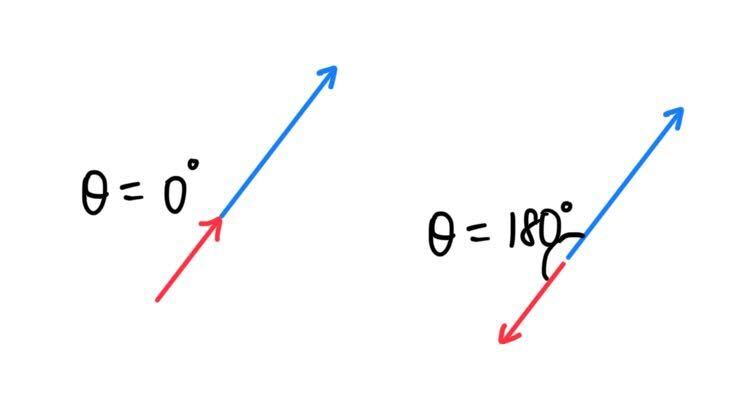
- $\vec{a}=c\,\vec{b} \; (c>0)$ → $\theta = 0º$
- $\vec{a}=c\,\vec{b} \; (c<0)$ → $\theta = 180º$
▶ 수직 벡터 : 두 벡터 $\vec{a}$, $\vec{b}$ 사이의 각도가 90º 인 경우
- $\vec{a} · \vec{b} = ||\vec{a}||\,||\vec{b}||\, cos(90º)$
- $cos(90º)=0$이기 때문에 $\vec{a} · \vec{b}=0$임
- 만약 $\vec{a}$와 $\vec{b}$가 영벡터가 아니면서 내적값이 0이면 두 벡터는 수직임
- 그렇지 않으면, ($\vec{a} · \vec{b}=0$) 내적값이 0일 때 '직교한다'라고만 할 수 있음
- 벡터가 0이 아니라면 '수직'이면서 '직교'라고 할 수 있음
- (참고) 영벡터는 모든 벡터와 직교함
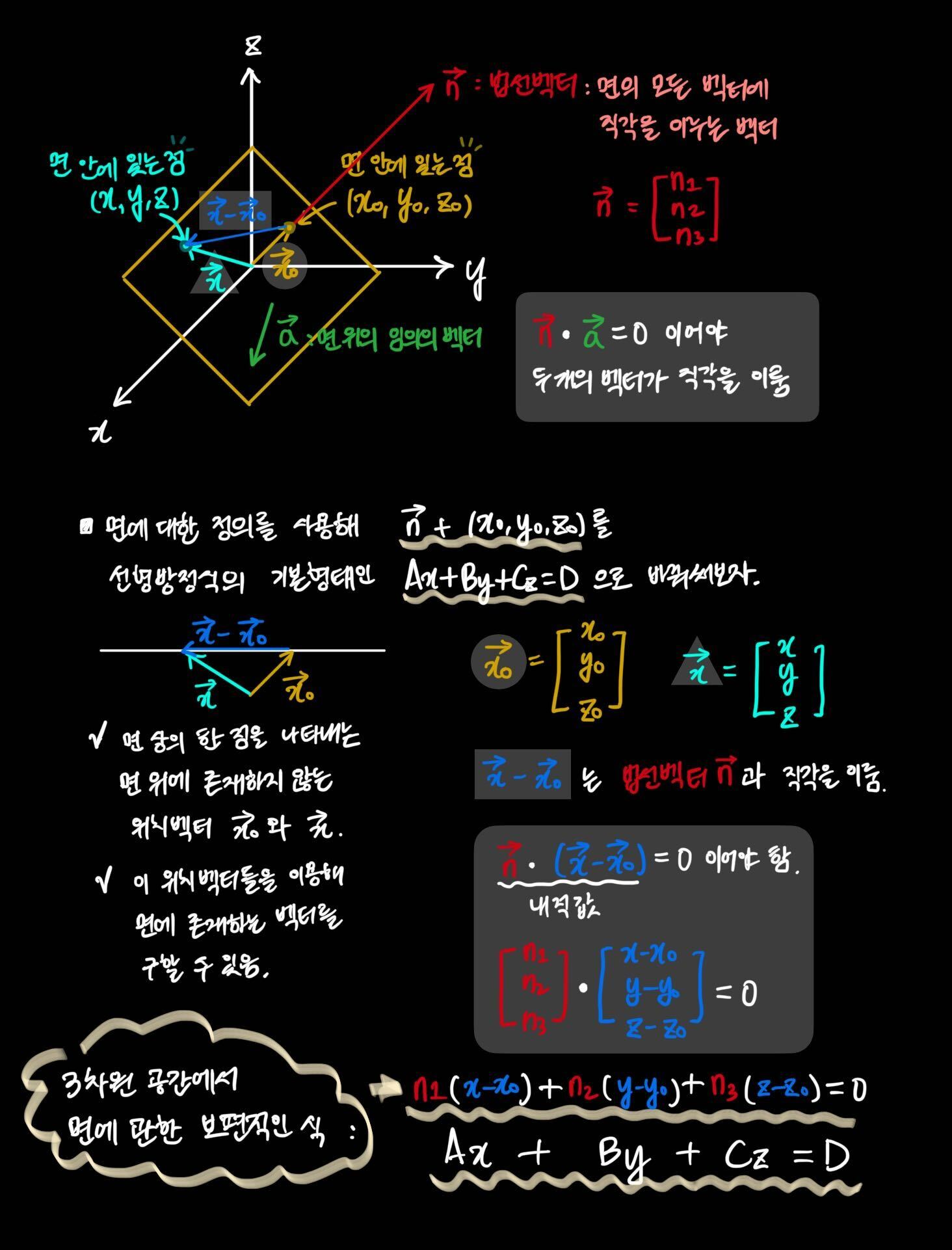
# 점과 법선벡터를 이용해 $\mathbb{R}^3$에서 평면 정의하기
▶ 법선벡터 n(normal vector) : 면에 직각을 이루는 벡터 (면의 모든 벡터에 직각을 이룸)
$\vec{n} · \vec{a}=0$일 경우에 한해서만 두 개의 벡터가 직각을 이룸
▶ 3차원 공간에서의 면의 방정식
# 벡터의 외적이란?
내적은 어느 차원($\mathbb{R}^n$)에서든지 정의가 되어있음 → 내적의 결과는 스칼라
외적은 오직 $\mathbb{R}^3$에서만 정의됨 → 외적의 결과는 또 다른 벡터



# 증명 : 외적과 각의 사인값 사이의 관계
$\vec{a} · \vec{b} = ||\vec{a}||\,||\vec{b}||\,cos\theta$

외적을 계산하면 벡터를 얻을 수 있음
외적의 절댓값을 구하면 스칼라 값을 얻을 수 있음
$||\vec{a}\,x \,\vec{b}|| = ||\vec{a}||\,||\vec{b}||\,sin\theta$
- $||\vec{a}\,x\,\vec{b}||^2 = ||\vec{a}||^2\, ||\vec{b}||^2\,(1-cos^2\theta)$
- $sin^2\theta + cos^2\theta = 1$
# 내적과 외적의 비교 / 직관
$\vec{a} · \vec{b} = ||\vec{a}||\,||\vec{b}||\,cos\theta$
$\sqrt{\vec{a} · \vec{b}}{||\vec{a}||\,||\vec{b}||} = cos\theta$
$\theta = arccos\, \sqrt{\vec{a} · \vec{b}}{||\vec{a}||\,||\vec{b}||}$
$||\vec{a}\,x \,\vec{b}|| = ||\vec{a}||\,||\vec{b}||\,sin\theta$
이 둘을 통해서 $\theta$를 어떻게 구하는지 확인
soh : 높이/빗변
cah : $cos\theta$는 이웃한 변/빗변과 같음 (수선의 발을 그으면, 삼각형을 만들 수 있음)
toa

내적은 두 벡터가 얼마나 같은 방향을 향하는지 말해줌
같은 방향을 향하는 벡터 길이의 곱
내적은 b방향으로 향하는 a의 일부에 b를 곱하는 것
$cos\theta$이 최대가 된다는 것은, 두 벡터가 동일선상에 있을 때임
$cos\theta \,0˚ = 1$
$\vec{a} · \vec{b} = ||\vec{a}||\, ||\vec{b}||$가 되는 것
외적은 얼마나 두 벡터가 수직인지를 말해줌
외적은 b방향의 수직인 a의 일부에 벡터 b를 곱하는 것
$sin\theta$이 최대가 된다는 것은,
$sin\theta \,90˚ = 1$이라서
$||\vec{a}\,x\,\vec{b}|| = ||\vec{a}||\,||\vec{b}||$는 두 벡터가 완벽히 수직인 경우를 말하는 것
두 벡터의 값이 수직일 떄 내적은 최소가 됨
두 벡터의 값이 동일선상에 있을 떄 외적은 최소가 됨
외적의 또 다른 해석
평행사변형의 넓이를 구하기
$Area = ||\vec{b}||\,x\, height$
$sin\theta = \sqrt{height}{||\vec{a}||} $ >> $height = ||\vec{a}||\, sin\theta$
$Area = ||\vec{b}||\,x\, ||\vec{a}||\, sin\theta$ = $||\vec{a}\,x\,\vec{b}||$
두 벡터의 외적의 절대값은,
세 번째 벡터의 크기는 두 벡터로 만들어지는 평행사변형의 넓이와 같음
# 평면방정식의 법선벡터

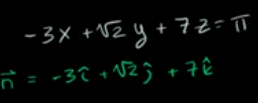
d 부분은 무엇이 와도 괜찮은 게
d에 따라 면이 이동되기는 해도 면이 기울어진 정도에는 아무 영향을 주지 않기 때문
다음엔
>> 3차원에서 어떠한 면과 임의의 점 사이의 거리를 구하는 방법 알아보기
>> 면까지의 최단거리를 구하는 방법
# 점과 평면 사이의 거리



# 평면 사이의 거리
두 평면 사이의 실제 거리 구하기
(한 평면 위의 한 점과 이 점에서 가장 가까운 다른 평면에서의 한 점 사이의 거리)
1) 한 평면 위의 점을 알아야 함
2) 그 점과 다른 평면 사이의 거리 구하기
'통계학, 인과추론 스터디 > 선형 대수학' 카테고리의 다른 글
| 선형 대수학 | Chapter 4. 행렬, 파트 1 : 행렬과 행렬의 기본 연산 (3) | 2024.12.04 |
|---|---|
| 선형 대수학 | Chapter 3. 벡터 응용 : 데이터 분석에서의 벡터 (0) | 2024.12.03 |
| 선형 대수학 | Chapter 2. 벡터, 파트2 : 벡터의 확장 개념 (0) | 2024.12.02 |
| 선형 대수학 | Chapter 1. 벡터, 파트1 : 벡터와 벡터의 기본 연산 (2) | 2024.11.29 |
| 선형대수학 Khan Academy | 1단원. 벡터와 공간(1) (0) | 2024.10.26 |




댓글