
1. 벡터
# 벡터
- 벡터는 크기와 방향을 동시에 나타냄
- ex) 속도
- 어디에서 시작하는지, 어디에 표현하는지는 상관 없음
- 좌표 (0,0)에서 시작을 했든 좌표 (5,5)에서 시작을 했든
크기와 방향만 같다면 다 같은 벡터임
- 좌표 (0,0)에서 시작을 했든 좌표 (5,5)에서 시작을 했든
# 실좌표공간
- n차원 실수좌표공간 $\mathbb{R}^n$ : 가능한 모든 실수값을 가지는 n-튜플
# 대수와 그래프를 이용한 벡터의 덧셈
 |
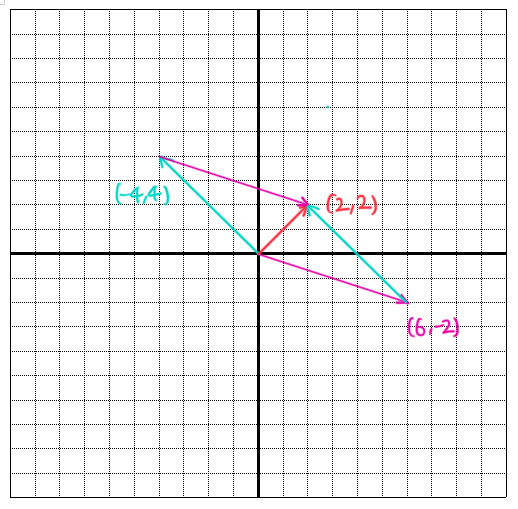 |
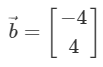 |
|
 |
# 벡터와 스칼라의 뺄셈
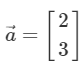 |
 |
 |
|
 |
# 벡터와 스칼라의 곱셈
- 벡터에 상수(스칼라)를 곱해주면 방향은 바뀌지 않고, 크기만 바뀜
- 벡터에 음수(스칼라)를 곱하면 방향이 바뀜
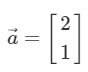 |
 |
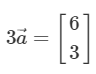 |
|
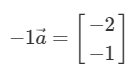 |
|
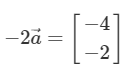 |
# 단위벡터(unit vector)
- 수평으로 한 칸
- 수직으로 한 칸
모든 벡터는 단위 벡터의 합으로 나타낼 수 있음
- ex) $\vec{b} = -1\hat{i} + 4\hat{j}$
단위벡터 i, j는 직교함 (서로 90도로 만남)
→ 어떤 $\mathbb{R}^2$ 위의 벡터든지 이 두 벡터로 나타낼 수 있음
→ 이 벡터들이 $\mathbb{R}^2$의 기저를 이룸
(사용 예시)
$ \vec{v} = \left[\begin{matrix} 2 \\ 3 \\ \end{matrix} \right] $
- 또는 $ \vec{v} = (2,3) $ 라고 표현 가능
이 $\vec{v}$를 단위 벡터로 표현하면, $ \vec{v} = 2\hat{i} + 3\hat{j} $ 이 됨.
(예제) $ \vec{v}=\left( 2, 7 \right)$ 방향의 단위벡터 구하기
 |
 |
# 직선의 매개변수 표현
- 동일 선상에 존재하는 벡터의 집합
- $\mathbb{R}^2$ 안의 모든 집합을 위치벡터로 그리면 기울기가 있는 한 직선이 됨 → 같은 기울기의 직선
- 기울기가 같은 여러 직선을 표현하는 식 → y = ax + b
- $\vec{P_{1}}$ : 기준 벡터 (시작점)
- $\vec{P_{1}} - \vec{P_{2}}$ : 기울기
2. 선형결합과 생성
# 선형 결합과 생성
$ c_{1}v_{1} + c_{2}v_{2} + ... + c_{n}v_{n}, c_{1} \rightarrow c_{n} \in \mathbb{R} $
▶ 선형 결합 : 벡터들의 합의 결합
벡터들에 상수곱을 한 것의 결합 (벡터끼리의 곱을 말하는 게 아님 주의)
$span(v_{1}, v_{2}, ..., v_{n}) - (c_{1}v_{1}+c_{2}v_{2}+...+c_{n}v_{n} | c_{n} \in \mathbb{R}, 1<= i <= n) $
▶ 생성 : 벡터의 선형결합으로 나타낼 수 있는 모든 벡터를 의미
- 각각의 벡터를 임의의 실수만큼 상수배하고 다 더함. 이런 선형결합을 다 모은 집합이 벡터들의 생성임
- $\mathbb{R}^n$ 위의
모든벡터를 $c_{1}$부터 $c_{n}$의 선형결합으로 나타낼 수 있다는 것을 의미
모든벡터
(※주의) 벡터 n개를 아무렇게나 잡아도 $R^2$ 전체를 생성하는 걸까? No!
→ 전체를 생성하지 못하는 n개의 벡터도 있음- ex. 영벡터의 생성은 영벡터 하나뿐임
영벡터 자신의 선형결합으로 얻을 수 있는 벡터는 영벡터 자신 뿐임
- ex. 영벡터의 생성은 영벡터 하나뿐임
- 임의의 벡터 a의 생성은 a의 크기를 바꾸면서 얻는 직선임 (a의 생성은 그냥 직선임)
만약 벡터 두 개의 생성이 $R^2$이 된다면 두 벡터는 같은 직선상에 있으면 안됨
3. 선형종속과 독립
# 선형독립이란?
▶ 선형종속 : 집합의 한 벡터를 다른 벡터의 선형결합으로 나타낼 수 있는 경우
즉, 직선을 벗어나게끔 하는 새로운 차원이 주어지지 않는 경우임
- $ \left[\begin{matrix} 2 \\ 3 \\ \end{matrix} \right] $ *2 → $ \left[\begin{matrix} 4 \\ 6 \\ \end{matrix} \right] $
▶ 선형독립 : 집합의 한 벡터를 다른 벡터의 선형 결합으로 나타낼 수 없는 경우
- $ \left[\begin{matrix} 7 \\ 0 \\ \end{matrix} \right] $ ⊥ $ \left[\begin{matrix} 0 \\ -1 \\ \end{matrix} \right] $
- 어떤 상수를 곱해도 서로의 벡터값을 얻을 수 없는 구조임
- 어떤 선형결합으로도 서로의 벡터값이 나오지 않는 경우 → 새로운 방향이 주어지는 것
# 선형독립 더 알아보기
벡터에 곱하는 상수 $c_{1}, ..., c_{n}$ 중 적어도 하나가 0이 아니라면 선형 종속임
→ 적어도 하나가 0이 아닌 경우 이 한 벡터는 다른 벡터의 결합으로 표현 가능하게 되어버림
반면, 모든 상수가 0인 방법 외에 방정식을 만족시킬 수 있는 방법이 없다면 이건 선형독립임
→ $c_{1}, ..., c_{n} = 0$
→ 이 중 어느 벡터도 나머지 벡터의 결합으로 표현될 수 없다는 것
$ c_{1}[\left[\begin{matrix} 2 \\ 1 \\ \end{matrix} \right] + c_{2}[\left[\begin{matrix} 3 \\ 2 \\ \end{matrix} \right] = 0 $
- $2*c_{1} + 3*c_{2} = 0$이고, $1*c_{1} + 2*c_{2} = 0$는 0임을 알 수 있음
- 이 두 방정식을 통해 $c_{1}$과 $c_{2}$를 구해보면 0이 나옴
즉, 이 방정식을 만족하는 답은 $c_{1}$과 $c_{2}$가 0일 때 뿐임 - 따라서 이것은 선형독립인 집합임 → $span(S) = \mathbb{R}^2$ : 이 벡터들의 생성이 $\mathbb{R}^2$임
4. 부분공간과 부분공간의 기저
# 선형 부분공간
- $\mathbb{R}^{n}$ : $\mathbb{R}^n$의 부분공간
- $V$ : $\mathbb{R}^{n}$의 부분집합
- $V$가 부분공간이거나 $\mathbb{R}^{n}$의 선형 부분공간이는 것의 의미
- $V$가 영벡터를 포함함 → [0, ..., 0]
- 만약 $x$가 $V$에 있고, $V$가 $\mathbb{R}^{n}$의 부분공간이라면
- $x$에 임의의 스칼라를 곱한 값 또한 $V$에 있음
→ $\vec{x}\,in\,V = c\vec{x}\,in\,V$ (스칼라 곱셈에 대해 닫혀있는 것) - $x$에 임의의 스칼라를 더한 값 또한 $V$에 있음
→ $\vec{a}\,in\,V, \vec{b}\, in\,V = \vec{a}+\vec{b}\,in\,V$ (스칼라 덧셈에 대해 닫혀있는 것)
- $x$에 임의의 스칼라를 곱한 값 또한 $V$에 있음
- $\mathbb{R}^n$의 부분집합이 있다면,
즉 영벡터를 포함하는 $\mathbb{R}^n$ 안의 어떤 벡터들의 집합을 가지고 있고,
곱셈과 덧셈에 대해 닫혀있다면 부분공간이 존재하는 것!- 선형 생성도 가능
- ex. [1,1]
- 벡터들의 선형결합을 표현하면 기울기가 일정한 선형 직선이 됨
- 영벡터를 포함하고 있음
- 곱셈과 덧셈에 대해 닫혀있음
- 선형 생성도 가능
- $V$가 부분공간이거나 $\mathbb{R}^{n}$의 선형 부분공간이는 것의 의미
# 부분공간의 기저
▶ 기저 : 어떠한 공간을 생성하는 데 필요한 최소한의 벡터 집합
→ 기저에는 불필요한 중복이 존재하지 않음
- 어떤 집합의 기저라는 것은,
이 벡터들이 부분공간을 생성하고, 부분공간의 어떤 벡터도 될 수 있으며, 그 벡터들은 선형독립이라는 것. - 보통 하나의 부분공간에 대해 무한 개의 기저가 존재함
$V = span(\vec{1}, \vec{2}, ... , \vec{n})$
- 이 벡터집합의 생성이 부분공간과 같거나, 부분공간을 생성하고, 동시에 모든 벡터가 선형독립일 때
이 벡터집합 S($ \vec{1}, \vec{2}, ... , \vec{n} $)가 부분공간 V의 기저라고 함
'통계학, 인과추론 스터디 > 선형 대수학' 카테고리의 다른 글
| 선형 대수학 | Chapter 4. 행렬, 파트 1 : 행렬과 행렬의 기본 연산 (3) | 2024.12.04 |
|---|---|
| 선형 대수학 | Chapter 3. 벡터 응용 : 데이터 분석에서의 벡터 (0) | 2024.12.03 |
| 선형 대수학 | Chapter 2. 벡터, 파트2 : 벡터의 확장 개념 (0) | 2024.12.02 |
| 선형 대수학 | Chapter 1. 벡터, 파트1 : 벡터와 벡터의 기본 연산 (2) | 2024.11.29 |
| 선형대수학 Khan Academy | 1단원. 벡터와 공간(2) (1) | 2024.11.04 |




댓글