통계학 Khan Academy | 9~10단원 (확률변수, 기하변수, 베르누이 분포, 푸아송 분포, 표본분포)

 

 

1. 9단원

1-1. 확률 변수

랜덤 프로세스를 통해 나온 확률값

P(X >= 5) 

• 이산확률변수
• 연속확률변수

 

▶ 확률변수에 대한 확률분포 만들기

(예시 문제) 화요일에 눈이 올 확률

P(화요일의 눈 높이)

표본공간 = {8, 10, 12, 14}

*표본공간 : 일어날 수 있는 모든 경우의 집합

• P(두 번 다 눈 옴 X =  10 + 2.5 + 1.5 = 14)  = 0.5 * 0.5 = 0.25
• P(월욜 눈 옴, 화욜 눈 안옴 X = 10 + 2.5 - 0.5 = 12) = 0.5 * 0.5 = 0.25
• P(월욜 눈 안옴, 화욜 눈 옴 X = 10 - 1.5 + 1.5 = 10) =  0.5 * 0.5 = 0.25
• P(월욜 눈 안옴, 화욜 눈 안옴 X = 10 - 1.5 - 0.5 = 8) = 0.5 * 0.5 = 0.25

 

▶ 기댓값

각 확률변수를 그에 따른 확률로 곱한 모든 수의 합

= 확률에 대한 가중합

 

▶ 이산확률분포의 분산과 표준편차

$Var(X) = \sum(확률변수X - 기댓값)^2$

 

$\sigma_x = \sqrt{Var(x)}$

 

[구하는 방법]

• 각 결과값과 평균의 차이를 제곱하기
• 제곱한 값들을 해당하는 확률과 곱하기
• 다 더하기 >> 분산
• 제곱근 취하기 >> 표준편차

 

1-2. 확률변수 합치기

▶ 독립성이 확률변수 합의 분산에 중요한 이유

만약 하루 중 자는 시간이 X, 깨어있는 시간이 Y라면 X + Y는 무조건 24시가 될 것

X에 어떤 수가 들어오든 Y는 24-X시간이 됨

그렇기 때문에 Var(X+Y)는 0이 됨 (하루가 24시라는 사실은 변할 일이 없기 때문)

 

▶ 확률변수 합, 차에 따른 분산 구하기

* 확률변수 합

$\mu_{X+Y} = \mu_X + \mu_Y$

 

$\sigma^2_{X+Y} = \sigma^2_X + \sigma^2_Y$

 

 

* 확률변수 차

$\mu_{X-Y} = \mu_X - \mu_Y$

 

$\sigma^2_{X-Y} = \sigma^2_X + \sigma^2_Y$

• 분산을 결합하기 이전에, 분산들이 독립이거나 독립성을 가정하기에 타당해야 함
• 두 확률변수를 빼더라도 분산은 그대로 더함
• 결합된 분포의 표준편차는 결합된 분산에 제곱근을 취해서 구할 수 있음

 

1-3. 이항확률변수

▶ 이항확률변수 조건

• 각 시행은 서로 독립적
  • 표본의 크기가 모집단의 10% 이하일 때 독립이 아니어도 독립일 때의 확률과 근사하게 됨
• 시행횟수(n)가 정해져 있음
• 사건의 결과가 '성공' 혹은 '실패'로 나뉨
• 각 시행의 성공 확률(p)는 항상 일정해야 함

▶ 일반화 공식

$P(정확한 k번 성공) = nCk * p^k * (1-p)^{n-k}$

 

▶ 이항확률분포함수(binompdf)와 이항누적확률분포함수(binomcdf) 

 

$P(X=4)$

 

$binompdf(n, p, k)$

 

 

$P(X<=4)$

 

$binomcdf(n, p, k)$

 

(예시문제)

박스 안에 상품이 있을 확률은 4상자 중에 1상자, 5개의 박스를 뜯어볼 때 상품을 발견할 경우가 2번 이하인 확률 구하기

 

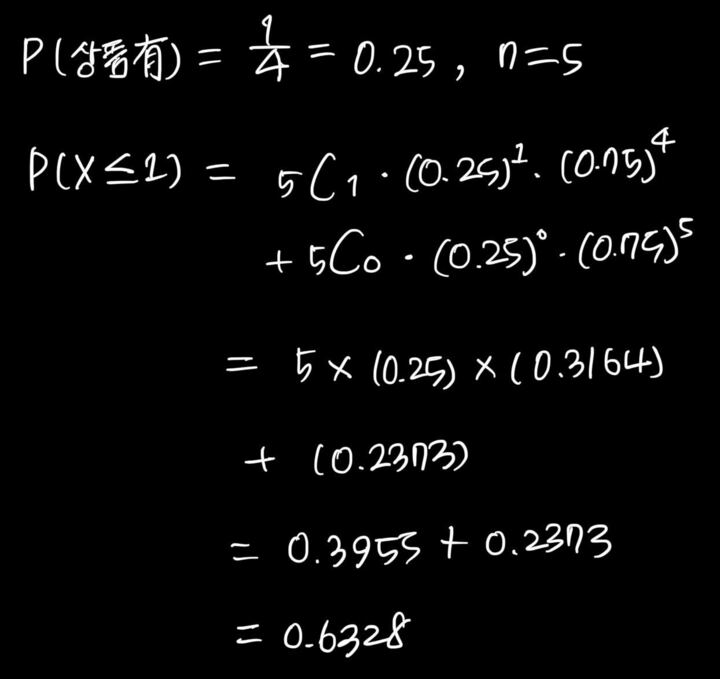1-4. 베르누이 분포의 평균과 분산에 대한 예제

▶ 베르누이 분포의 평균과 분산

$\mu = (1-p)*0 + p*1 = p$

 

$\sigma^2 = (1-p)(0-p)^2 + p(1-p)^2 = p-p^2 = p(1-p)$

 

$\sigma = \sqrt{p(1-p)}$

 

▶ 이항변수의 기댓값

$E(X) = nE(Y) = np$

 

▶ 이항변수의 분산

$Var(X) = nVar(Y) = n*p(1-p)$

 

1-5. 기하변수란?

▶ 기하확률변수

성공을 위해 얼마나 많은 시행이 필요한가?

• 시행은 독립
• 성공 확률은 매 시행마다 동일
• 고정된 시행 횟수 없음
• 구해야 하는 변수는 시행한 횟수

↔ 이항확률변수 : 유한한 시행횟수에서 얼마나 많은 성공을 했는가?

• 시행은 독립
• 성공 확률은 매 시행마다 동일
• 고정된 시행 횟수 있음
• 구해야 하는 변수는 성공 횟수

▶ 기하변수의 확률

(예시문제)

P(C=4) = (0.9^3) * (0.1*1) = 0.0729

 

▶ 누적 기하학적 확률

(예시문제)

1-(0.75)^3 = 0.58

 

▶ 기하확률분포함수(geometpdf)와 기하누적확률분포함수(geometcdf) 

$P(X=5)$

 

$geometpdf(n, X)$

 

 

$P(X<=5)$

 

$geometcdf(n, X)$

 

▶ 기하변수의 기댓값

독립사건이 발생할 확률 p인 기하확률변수의 기대값은 1/p

$E(X) = \frac{1}{p}$

 

1-6. 기댓값 더 알아보기

▶ 경험적 확률과 기댓값

기댓값 = 상대도수*확률변수

상대도수 = 절대빈도수 / 표본공간의 크기

 

▶ 계산된 확률과 기댓값

기댓값 = (모든 확률변수에 대한 대응되는 확률 * 확률변수) 총합

해당 사건의 확률 = 확률변수 * 해당 사건 경우의 수

 

▶ 큰 수의 법칙

큰 수의 법칙에 따르면 표본평균은 확률변수의 기댓값에 근접

$\bar{X_n} → E(X)$

n이 무한대에 가까워지면 표본평균이 모평균에 가까워진다

 

(예시문제) 계산된 확률과 기댓값

 

(예시문제) 기댓값을 통한 의사결정

• 버스 시간 준수 여부 + 버스 표 종류 별 상대도수 구하기
• 해당 상대도수에 10 곱하기 (문제에서 해당 표를 10개 산다고 했기 때문)
• '해당 버스표를 살 때의 기댓값'을 구하기 위해 버스표 별 비용을 곱해줌
  • 일반 버스 표 기댓값 : 일반 버스 표끼리 값 더해주기
  • 대기 버스 표 기댓값 : 대기 버스 표끼리 값 더해주기

 

(예시문제) 기댓값을 통한 의사결정

 

1-7. 푸아송 과정

▶ 푸아송분포

주어진 시간 내, 공간 내 k횟수만큼 성공할 확률

$P(X=k) = (n, k) (\lambda / n)^k * (1-\lambda/n)^n-k$

 

$limited_x → 무한대, (1 + a / x ) ^ 2 = e^a$

 

이항분포일 때,

$E(X) = \lambda = np$

 

$P(X=k) = limited_n → 무한대, (n, k) * (\lambda / n)^k * (1-\lambda / n)^n-k = \lambda / k! * e^-\lambda$

 

2. 10단원

2-1. 표본분포

표본으로부터 얻어지는 통계량들의 분포

 

▶ 편향

표본분포의 평균이 모수의 값과 동일할 때 통계량은 모수의 불편추정량임

즉, 평균적으로 통계량이 측정하고 있는 모수의 값과 동일할 때 통계량은 불평추정량

 

(예시문제)

정답 : 1번

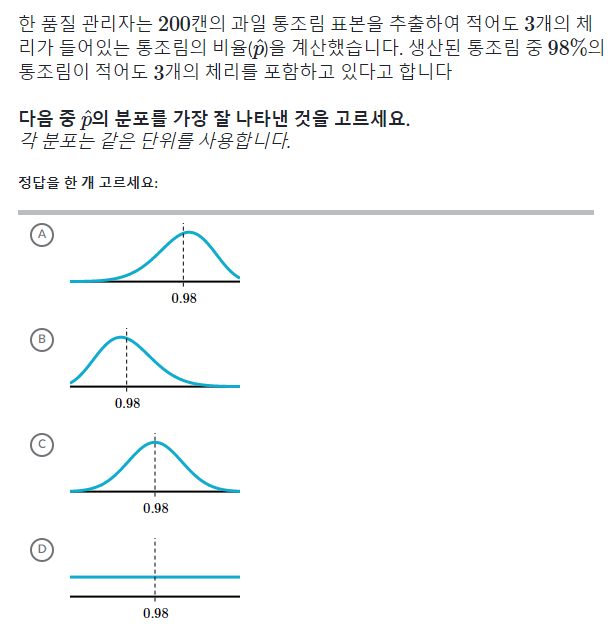
* 정규분포 조건 : p >= 10 이고, (1-p) >= 10

* '치우치다'의 의미 제대로 이해하기

: 생산된 통조림 중 98%가 적어도 3개의 체리를 포함하고 있음

하지만 몇몇 표본에는 통조림에 3개보다 적은 체리가 들어있을 수 있음

따라서 \hat p의 비율은 대부분의 경우 높을 것이고, 그래프는 비율이 더 낮은 쪽으로 치우칠 것 

 

2-2. 표본비율의 표본분포

* 정규분포 기준 (np >= 10 , n(1-p) >= 10)

: 적어도 10개의 성공과 10개의 실패가 예상되어야 함

$\mu_x = np$

 

$\sigma = \sqrt{n*p*(1-p)}$

 

$\mu_{\hat p} = np / n = p$

 

$\sigma_ {\hat p} = \sigma_x / n = \sqrt{p(1-p)/n}$

표본비율의 표본분포 평균은 모비율과 같음

 

2-3. 표본평균의 표본분포

▶ 중심극한정리

샘플 사이즈가 무한대로 갈 때 정규분포가 됨

비록 모집단의 분포가 정규분포가 아닐지라도 표본평균의 분포는 정규분포를 따를 것

 

▶ 표본평균의 표본분포

* 표본평균의 표본분포의 평균

$\mu_{\bar{X}}$

 

▶ 평균의 표준오차

샘플 사이즈가 커지면 커질수록 표준편차는 작아짐

표본평균 표본분포의 표준편차는 평균의 표준편차라고도 하고, 평균의 표준오차라고도 함

* 표본평균 표본분포의 분산

$\sigma_{\bar{X}}^2 = \frac{\sigma^2}{n}$

* 표본평균 표본분포의 표준편차

$\sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}}$