통계학 Khan Academy | 확률과 통계 4~6단원 (자료분포 모델링, 연구방법론)

 

1. 4단원 : 자료분포 모델링

▶ z-score

평균이 표준편차의 몇 배가 떨어져 있는지를 나타냄

평균과 해당 값의 간격이 표준편차의 몇 배인지

$z = \frac{x-\bar x}{\sigma} $

 

(예시) 

• z = -2.3 : 평균이 표준편차 -2.3만큼 떨어져있음
• z = 1.5 : 평균이 표준편차 1.5만큼 떨어져있음 

z-score는 검정색 선 상의 한 값

 

▶ 정규분포와 경험법칙

68% - 95% - 99.7%

 

(문제) 역사 시험 점수

 

 

▶ 분포의 이동, 변화

중심경향치(평균, 중앙값) 는 상수를 사칙연산(+, -, *, /) 하면 분포가 이동하거나 변함

• +, - : 분포의 중심경향치가 더하고 뺀 만큼 늘어남 (단, 분포 변화는 없음)
• *,  / :  분포의 중심경향치가 곱하고 나눈만큼 커지고, 작아짐 (분포 변화 있음)

산포도(표준편차, IQR, 범위) 는 상수를 + - 할때는 변하지 않고, * % 일 때는 변함

• +, - : 중심경향치의 이동만 있을 뿐 분포의 변화는 없으므로 동일
• *,  / : 중심경향치 뿐 아니라 분포의 변화도 있어서 곱하고, 나눈만큼 커지고, 작아짐

 

(문제) 화씨 → 섭씨로 변환할 때의 평균과 표준편차의 변화

• 평균 = 104 F
• 표준편차 = 2 F

정답 : 평균은 식의 모든 계산이 적용된 값, 표준편차는 *5/9 만 해준 값

 

2. 5단원 : 자료분포 모델링

▶ 결정계수 (r제곱)

변수 x에 대한 회귀분석을 통해 나타나는 설명 변수  y가 변화하는 비율입니다.

 

*결정계수는 예측 오차가 얼마나 줄어든 건지 측정하는 것

$ r^2 = \frac{회귀 없이 측정한 오차 - 회귀 사용 후 오차}{회귀없이 측정한 오차} * 100$

 

회귀 없이 측정한 오차

대응하는 x값 없이 y값을 예측할 때 가장 적절한 방법은 y값의 평균을 예측하는 것

y값 평균 : 검정색 선

이 때, y값의 평균과 각 값들이 떨어져 있는 거리(잔차)의 제곱합 = 41.1879

 

회귀로 예측하기

대응하는 최소 제곱 회귀선

최소제곱 회귀선

 

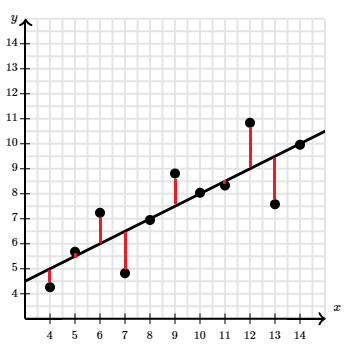
최소제곱 회귀선의 방정식  (r과 r제곱)

$\hat y = 0.5x + 1.5 $ $ r = 0.816 $ $ r^2 = 0.6659 $

 

정리

회귀를 사용하지 않았을 때의 측정 오차 = 41.1879

회귀를 사용했을 때의 측정 오차 = 13.7627

$ r^2 = \frac{41.1879 - 13.7627}{41.1879} * 100 = 약 66.59%$

 

이 값은 r제곱(결정계수)과 같은 수치 

>> 변수 y를 평균으로 예측했을 때에 비해 최소제곱 회귀를 사용해서 예측한 오차가 얼마나 더 줄었는지 알 수 있는 수치 

 

3. 6단원 : 연구방법론

▶ 표본연구와 관측연구

표본연구의 목적은 모집단의 특정한 모수를 추정하는 것

관측연구와 실험연구의 목적은 모집단의 두 모수를 비교하는 것

 

▶ 표본 샘플링

임의 표본으로 뽑아놓고, 임의 배정을 안 할 수도 있는 것..

 

선형회귀 식

 

잔차