인과추론 | Chapter 2. 무작위 실험 및 기초 통계 리뷰

 

2.1 무작위 배정으로 독립성 확보하기

잠재적 결과와 처치가 독립인 경우, 연관관계는 인과관계와 동일해짐

$(Y_0, Y_1) ⊥ T$

• 처치와 결과 사이의 독립성을 말하는 것이 아님
  • 처치와 결과가 독립적이라는 것은 처치가 있든 없든 결과가 달라지지 않는다는 것. 
• 처치와 잠재적 결과가 독립적이라는 것
  • $Y_1 ⊥ T$ : 실험 대상이 처치 받았더라면 관측되었을 결과가 실제로 처치 받앗는지 여부와 무관하다는 뜻
  • $Y_0⊥ T$ : 실험 대상이 처치 받지 않앗을 경우 관측되었을 결과가 실제 처치 여부와 무관하다는 뜻
  • 즉, 실제 관측된 결과 Y는 처치 여부에 따라 달라지는 것 → 실험군과 대조군이 비교 가능함을 뜻함

처치를 무작위로 배정(RCT : randomized control trial) 하면 실험군과 대조군 간의 유일한 차이는 처치밖에 없게 됨
→ 두 그룹의 결과 차이는 해당 처치에 따른 것으로 볼 수 있게 됨

2.2 A/B 테스트 사례

무작위 배정이 제대로 이루어졌는지 확인하려면 실험군과 대조군이 처치 받기 전 동일한지 확인해봐야 함

두 그룹이 비슷한지 평가하는 방법 중 한가지 → 실험 대상 집단 사이의 정규화 차이 계산

$\frac{\hat\mu_{tr} - \hat\mu_{co}}{\sqrt{\hat\sigma^2_{tr} + \hat\sigma^2_{co} / 2}}$

 

# A/B 테스트 검정 계산기

https://abtestguide.com/calc/

A/B-Test Calculator - Power & Significance - ABTestGuide.com

 

2.3 이상적인 실험

무작위 통제 실험(RCT) 은 인과효과를 파악하는 가장 신뢰할 수 있는 간단한 방법이지만

많은 시간과 비용이 들고, 비윤리적일 수 있음

하지만 RCT는 실험 없이도 인과효과를 발견할 수 있는 방법에 대한 통찰을 줌

 

2.4 가장 위험한 수식

RCT는 인과관계를 식별할 때 유용하지만, 실험의 표본크기가 작으면 두 번째 단계인 추론이 어려울 수 있음

• 표준편차에 대한 드무아브르의 공식 →  '얼마나 부정확한가'를 지적해줌

$SE = \frac{\sigma}{\sqrt{n}}$

SE : 평균의 표준오차 / $\sigma$ : 표준편차 / $n$ : 표본 크기

 

• 추정값의 분산 →  불확실성을 정량화하는 방법 중 한 가지

불확실성에는 체계적 오차와 무작위 오차가 있음

• 체계적 오차(systematic error) : 모든 측정값에 동일한 방식으로 영향을 미치는 일관된 편향
• 무작위 오차(random error) : 우연히 생긴 예측 불가능한 변동 → 표본크기가 증가할수록 줄어듦

 

2.5 추정값의 표준오차

처치의 효과가 우연에 의한 것인지 아닌지 확신할 만큼 표본크기가 충분한지

처치의 효과가 통계적으로 유의한지 알고싶으면 표준오차 SE를 추정해야 함

 

표준편차 추정 공식

$\hat\sigma = \sqrt{\frac{1}{N-1} \sum\limits_{i=1}^{N}(x-\bar{x}^2}$

$\bar x$ : $x$ 의 평균

 

 

2.6 신뢰구간

신뢰구간은 추정값에 대한 불확실성을 나타내는 방법

추정값의 표준오차는 신뢰도를 나타내는 척도

 

현실에서는 여러 데이터셋에 동일한 실험을 시뮬레이션 하기 어려움

대신 하나의 데이터셋에서 여러 실험을 시뮬레이션 해볼 수 있음

 

각각의 실험에서 각 분포의 평균을 구할 수 있게되고,

표본평균들의 분포는 중심극한정리 (CLT : central limit theorem)에 따라 정규분포로 근사하게 됨

분포의 표준오차(표본평균 분포의 표준편차)를 이용해 실제 평균에 대한 95% 신뢰구간을 구성할 수 있음

• 추정값 $\mu$ 을 중심으로 신뢰구간을 구성하는 방법 $\hat\mu ± z*SE$
  • 여기서 $z$는 정규분포의 질량 중 $\alpha$ %에 해당하는 값

100번 반복 샘플링 시 95번은 모평균이 ± 2 SE 안에 포함되어 있다는 의미 (참고: https://angeloyeo.github.io/2021/01/05/confidence_interval.html)

• 95% 신뢰구간의 의미
  여러 실험을 수행하고 각 실험에서 95%의 신뢰구간을 구성한다면
  실제 평균이 100번 중 95번은 신뢰구간 내에 속함을 의미
  • 표본크기가 작을수록 신뢰구간은 넓어짐
  • 추정값에 신뢰구간을 반드시 넣어야 함!
  • 각 그룹 간 신뢰구간이 겹치지 않았다는 것은 그룹 간의 차이가 우연이 아닐 가능성이 높다는 것
    • 통계적으로 유의한 차이가 있음을 의미함
  • 반대로 각 그룹 간 신뢰구간이 겹친다면 통계적으로 유의하지 않음을 의미 
    • 단정지을 수는 없음

 

2.7 가설검정

불확실성을 반영하는 또 다른 방법은 가설검정을 통한 결과 제시

가설검정은 '두 그룹 간의 평균 차이가 0(혹은 다른 특정값)과 통계적으로 유의한 차이가 있는가?'라는 질문을 다룸

• 분포의 평균 : 두 분포 평균의 합이나 차 계산
• 분포의 분산 : 항상 두 분산의 합으로 계산

귀무가설을

• x% 신뢰구간을 이용해 기각할 수도 있고,
• 검정통계량을 통해 기각할 수도 있음

 

2.8 p값

p값은 귀무가설이 참이라고 가정할 때 관측된 결과보다 더 극단적인 결과가 실제로 관측될 확률임

즉, $P(H_{0} | data)$ 가 아니라 $P(data | H_{0})$

 

 

2.9 검정력

귀무가설을 올바르게 기각할 확률을 검정력(power of the test)이라고 함

• $\alpha$ = 0.05인 경우,
  매개변수 추정값과 귀무가설 사이의 차이 $\delta$ 는 최소한 0에서 1.96SE만큼 떨어져 있어야 함
  • 즉, $\delta$  - 1.96SE > 0 $ 이어야 통계적으로 유의하다고 할 수 있음
• 검정력($1-\beta$)의 일반적인 기준은 80%임
  
  • 즉, 95%의 신뢰구간의 하한이 0보다 높은 경우가 전체 실험의 80%에 달해야 한다는 것

 

[질문]

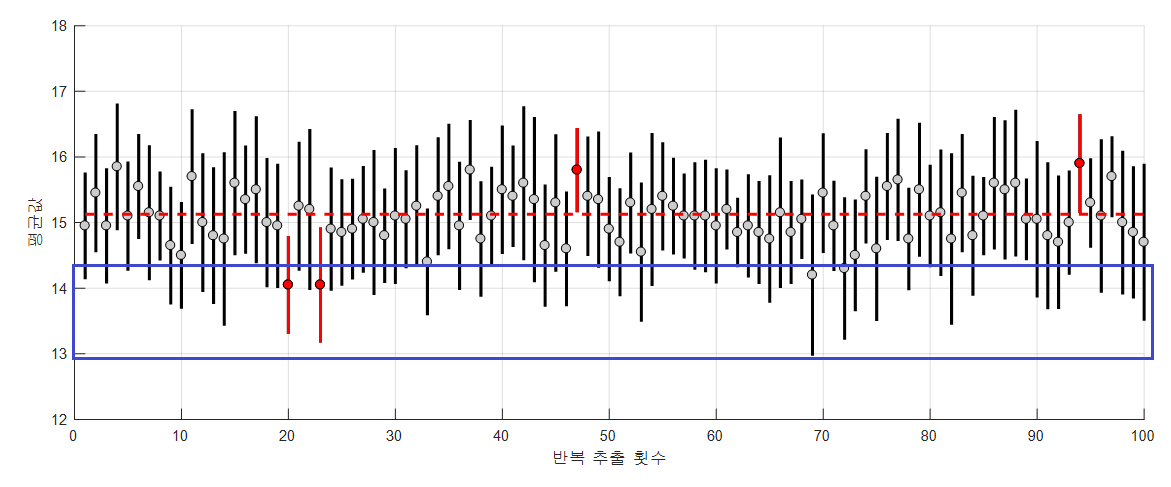
(p.96) 눈에 띄는 것은 95% 신뢰구간의 하한이 정규분포를 따른다는 것입니다.

표본평균의 분포처럼 95% 신뢰구간 하한의 분포는 표준오차와 같은 분산을 가지고 평균은 $\delta - 1.96SE > 0$입니다. 이는 단지 표본평균의 분포를 1.96SE만큼 이동한 것에 불과합니다. 따라서 $\delta - 1.96SE > 0$ 경우가 80%가 되려면, 차이가 0에서 1.96SE + 0.84SE만큼 떨어져야 합니다.

1.96은 95% 신뢰구간을 확보하기 위한 값이고, 0.84는 신뢰구간의 하한이 0을 초과하는 경우가 전체의 80%에 해당하도록 하기 위한 값입니다.

$\alpha$ = 0.05인 경우, 추정값과 귀무가설 사이의 차이인 $\delta$ 는 최소한 0에서 1.96SE만큼 떨어져 있어야 함 (이해O)

$\delta - 1.96SE$ 가 95% 신뢰구간의 하한 (이해O)

따라서 결과가 통계적으로 유의하다고 하려면 $\delta - 1.96SE > 0$  (이해O) → 결국 $\delta > 1.96SE$ 이고,

$ \delta $ 가 1.96SE보다 커진다는 건 차이가 통계적으로 유의미해서 귀무가설을 기각할 정도라는 것을 의미한다고 이해함

 

검정력($1-\beta$) 은 올바르게 기각할 확률이고,

80%의 검정력을 달성한다는 건, 귀무가설이 거짓일 때 80%의 확률로 귀무가설을 기각해야 한다는 것

 

2.10 표본 크기 계산

귀무가설이 거짓일 때 귀무가설과 관측된 추정값의 차이인 $\delta$ 를 감지할 수 있어야 함

• ex) 2.8SE = 1.96SE + 0.84SE
  예를 들어 8% 차이를 감지하고자 하는 실험 설계를 하고자 한다면, 8% = 2.8SE 를 감지할 표본 크기를 확보해야 함
  • 차이에 대한 표준오차 공식은 $SE = \sqrt{SE_{1}^{2} + SE_{2}^{2}}$ 
  • 실험군의 표준오차는 주어지지 않았지만, 실험군과 대조군의 분산이 같을 것이라고 가정할 수 있음
    그랬을 때 $SE = \sqrt{2SE^{2}} = \sqrt{2\sigma / n} = \sigma\sqrt{2/n}$
  • 이를 감지 가능한 차이에 연계하면 80%의 검정력과 95%의 신뢰도를 원할 때 표본크기를 결정하는 공식은
    $\delta = 2.8\sigma\sqrt{2/n}$ 이고 n에 대한 공식을 만들면 $16\sigma^{2} / \delta^{2}$